How To Find A Parabola Vertex
Graphing Quadratic Functions: The
Leading Coefficient / The Vertex (folio ii of 4)
Sections: Introduction, The meaning of the leading coefficient / The vertex, Examples
![]()
The general form of a quadratic is " y = ax two + bx + c ". For graphing, the leading coefficient " a " indicates how "fat" or how "skinny" the parabola will be.
For | a | > 1 (such as a = 3 or a = –4 ), the parabola volition exist "skinny", because information technology grows more than quickly (three times equally fast or four times as fast, respectively, in the case of our sample values
of a ).
For | a | < 1 (such as a = 1/3 or a = –1/4 ), the parabola will be "fat", because it grows more slowly (one-tertiary as fast or i-quaternary as fast, respectively, in the examples). As well, if a is negative, and then the parabola is upside-down.
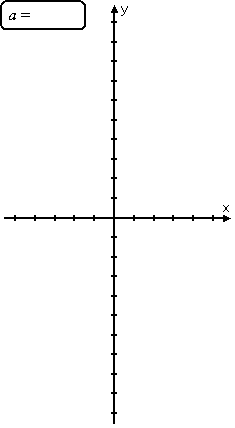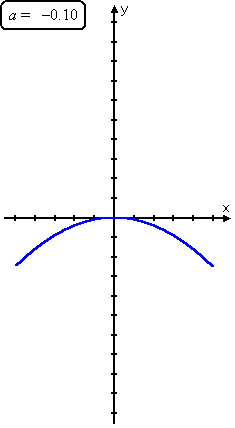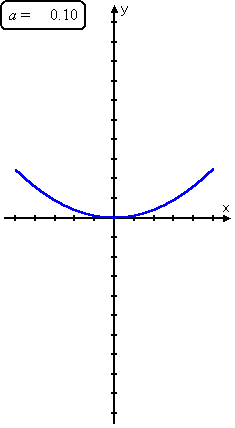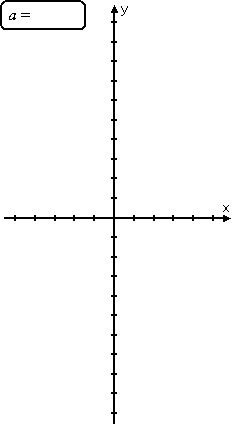
| You can encounter these trends when you await at how the curve y = ax 2 moves as " a " changes: | |
Equally you can see, as the leading coefficient goes from very negative to slightly negative to zilch (not really a quadratic) to slightly positive to very positive, the parabola goes from skinny upside-down to fat upside-downwardly to a straight line (called a "degenerate" parabola) to a fatty right-side-upwards to a skinny correct-side-up. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
There is a simple, if slightly "dumb", fashion to remember the difference between right-side-upward parabolas and upside-down parabolas:
This tin can be useful information: If, for case, you lot have an equation where a is negative, merely you're somehow coming up with plot points that make it look like the quadratic is correct-side-up, and then yous will know that you need to go back and check your work, because something is wrong .
Parabolas always take a lowest point (or a highest bespeak, if the parabola is upside-down). This bespeak, where the parabola changes direction, is called the "vertex".
If the quadratic is written in the course y = a(10 – h)ii + k, then the vertex is the indicate (h, k) . This makes sense, if y'all think near information technology. The squared part is always positive (for a right-side-up parabola), unless it'due south zero. So you'll e'er have that fixed value k , and then you'll always be adding something to it to make y bigger, unless of course the squared part is zero. So the smallest y can possibly be is y = k , and this smallest value will happen when the squared part, x – h , equals aught. And the squared office is naught when ten – h = 0 , or when x = h . The aforementioned reasoning works, with k existence the largest value and the squared part always subtracting from information technology, for upside-downwards parabolas.
(Note: The " a " in the vertex form " y = a(x – h)two + k " of the quadratic is the same as the " a " in the common class of the quadratic equation, " y = ax 2 + bx + c ".)
Since the vertex is a useful point, and since you can "read off" the coordinates for the vertex from the vertex form of the quadratic, y'all can meet where the vertex form of the quadratic can be helpful, especially if the vertex isn't one of your T-chart values. However, quadratics are not commonly written in vertex grade. You can complete the square to convert ax 2 + bx + c to vertex form, just, for finding the vertex, it's simpler to just utilize a formula . (The vertex formula is derived from the completing-the-square process, just equally is the Quadratic Formula. In each example, memorization is probably simpler than completing the foursquare.)
For a given quadratic y = ax 2 + bx + c , the vertex (h, 1000) is found by computing h = –b /2a , and and then evaluating y at h to detect k . If y'all've already learned the Quadratic Formula , you may observe it easy to memorize the formula for k , since information technology is related to both the formula for h and the discriminant in the Quadratic Formula: yard = (4ac – b 2 ) / 4a .
- Find the vertex of y = 3x 2 + 10 – 2 and graph the parabola.
To find the vertex, I expect at the coefficients a , b , and c . The formula for the vertex gives me:
h = –b /2a = –(1)/ii(3) = –one/half-dozen
So I can detect k by evaluating y at h = –1/6 :
1000 = three( –ane/half dozen )two + ( –1/half-dozen ) – 2
= 3/36 – 1/6 – ii
= 1/12 – ii/12 – 24/12
= –25/12
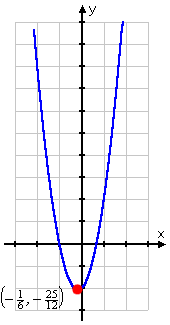
So now I know that the vertex is at ( –1/half-dozen , –25/12 ) . Using the formula was helpful, because this point is not i that I was likely to get on my T-chart.
| I need additional points for my graph: | |
| Now I can do my graph, and I will label the vertex: | |
When you lot write down the vertex in your homework, write down the exact coordinates: "( –1/half-dozen , –25/12 ) ". But for graphing purposes, the decimal approximation of " (–0.two, –two.1) " may be more helpful, since it'southward easier to locate on the axes.
The only other consideration regarding the vertex is the "centrality of symmetry". If you look at a parabola, you'll observe that you could draw a vertical line right upwardly through the middle which would split the parabola into ii mirrored halves. This vertical line, right through the vertex, is called the axis of symmetry. If you're asked for the axis, write downward the line " x = h" , where h is simply the x -coordinate of the vertex. So in the instance above, and so the axis would be the vertical line ten = h = –1/6.
Helpful note: If your quadratic's x -intercepts happen to be squeamish neat numbers (so they're relatively easy to piece of work with), a shortcut for finding the axis of symmetry is to note that this vertical line is always exactly between the two ten -intercepts. And so you can just average the two intercepts to get the location of the axis of symmetry and the x- coordinate of the vertex. Yet, if y'all have messy x -intercepts (as in the example above) or if the quadratic doesn't actually cantankerous the x -axis (as you'll see on the next page), so y'all'll need to employ the formula to find the vertex.
<< Previous Meridian | 1 | 2 | iii | four| Return to Index Next >>
| Cite this article equally: | Stapel, Elizabeth. "Graphing Quadratic Functions: The Leading Coefficient / The Vertex." Purplemath. Bachelor from |
Source: https://www.purplemath.com/modules/grphquad2.htm
Posted by: lentzoneverse.blogspot.com

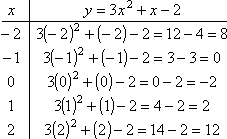

0 Response to "How To Find A Parabola Vertex"
Post a Comment